Opgave 1 – Vergelijking oplossen

Bereken exact de oplossingen van \(  \cos(4x-\frac{1}{4} \pi) = -\sin(3x+1\frac{3}{4} \pi) \) op \([0,\pi]\).

Opgave 2 – Van \( \sin(x) \) naar \( \sin(2x) \)

Gegeven is dat \( \sin(x)=\frac{3}{5} \). Er zijn twee mogelijke waarden voor \( \sin(2x) \). Bereken exact deze twee mogelijke waarden.

Opgave 3 – Bewijzen

Toon aan dat \( \tan^2(x)=\frac{1-\cos(2x)}{1+\cos(2x)} \)

Opgave 4 – Puntsymmetrie

Toon aan dat \(f(x)=\sin(2x)-\cos(x) \) puntsymmetrisch is in het punt \( (\frac{1}{2} \pi ,0)\).

Opgave 5 – Oppervlakte

Het vlakdeel \( V \) wordt ingesloten door de grafiek van \(f(x)=\sin^2(2x)-\frac{1}{2} \) op het domein \( [0, \frac{1}{2} \pi]\) en de x-as. Bereken exact de oppervlakte van het vlakdeel \( V\).

Opgave 6 – Samengestelde trilling

Bereken de periode van de samengestelde trilling \(u(t)=4\sin(3 \pi t)+\cos(6 \pi t)-\sin(12 \pi t)\) met \(t\) in seconden.

Opgave 7 – Punt op cirkel

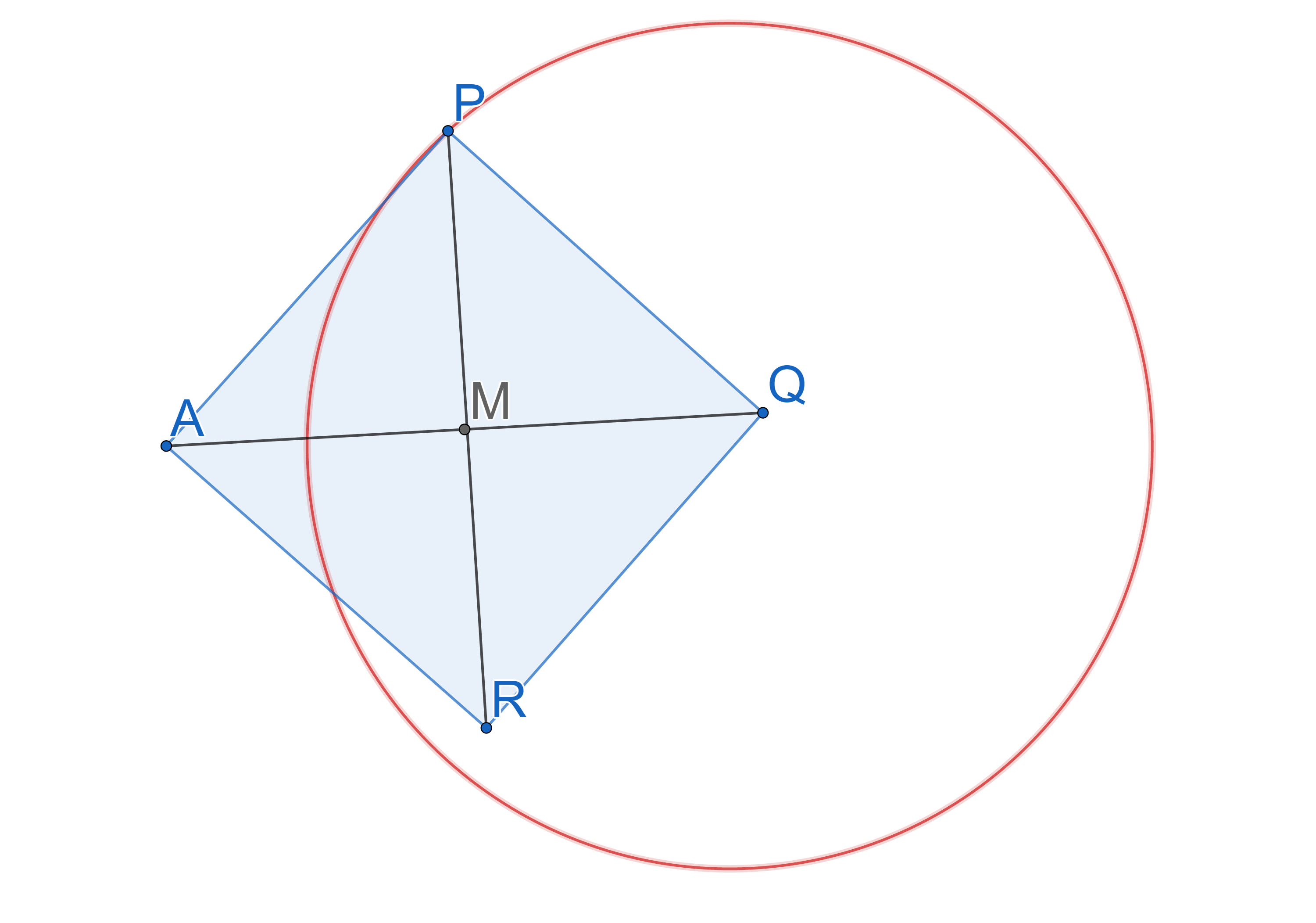
Het punt \(P\) doorloopt een cirkel met middelpunt \( (4,1) \) tegen de klok in. Op \( t=0 \) is \(P\) in het punt \( (7,1) \). Op \(t=6 \) is \(P\) in het punt \( (4,-2) \). 

a. Stel de bewegingsvergelijkingen op van punt \(P\).

Gegeven is het punt \(A(0,1)\). Lijnstuk \(AP\) is een zijde van het vierkant \(APQR\), zoals weergegeven in het figuur. Het punt \(M\) is het middelpunt van het vierkant.

b. Stel de bewegingsvergelijkingen op van het punt \(M\).