Machten Herleiden
Bij het herleiden van machten houdt je rekening met de rekenregels voor machten en met de rekenvolgorde.

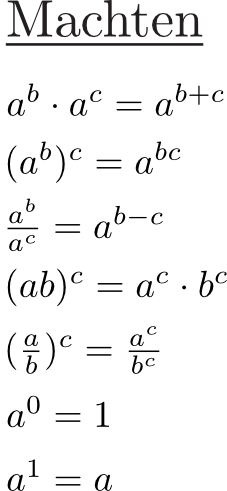
Opgave 1
Herleid \(A=(3q^4)^2-5q^3 \cdot 6q^5\)
Antwoord
\(A=-21q^8\)
Opgave 2
Herleid \(A=\frac{8p^2q^5}{2pq^2}+\frac{9pq^6}{(3q)^4}\)
Antwoord
\(A=4pq^3+\frac{1}{9}pq^2\)
Opgave 3
Herleid \(B=\frac{20x^2y}{4xy}-\frac{(4x^7)^3}{(2x^4)^5}\)
Uitwerking
\(B=\frac{20x^2y}{4xy}-\frac{(4x^7)^3}{(2x^4)^5}=\frac{20x^2y}{4xy}-\frac{4^3 \cdot (x^7)^3}{2^5 \cdot(x^4)^{5}}\)
\(B=\frac{20x^2y}{4xy}-\frac{64x^{21}}{32x^{20}}=5x-2x\)
Dus \(B=3x\)
Opgave 4
Herleid \(C=(8xy)^2+4x \cdot 3xy^2\)
Uitwerking
\(C=(8xy)^2+4x \cdot 3xy^2 = 8^2 \cdot x^2 y^2+4 \cdot 3 \cdot x \cdot x \cdot y^2=64x^2 y^2+12x^2 y^2\)
Dus \(C=76x^2y^2\)
Opgave 5
Herleid \(D=\frac{(7x^3)^2 \cdot 2x}{(4x)^2}\)
Uitwerking
\(D=\frac{(7x^3)^2 \cdot 2x}{(4x)^2}=\frac{7^2 \cdot (x^3)^2 \cdot 2x}{4^2 \cdot x^2}= \frac{49x^6 \cdot 2x}{16x^2}=\frac{49 \cdot 2 \cdot x^6 \cdot x}{16x^2}=\frac{98x^7}{16x^2}\)
Dus \(D=6\frac{1}{8}x^5\)
